Computer Algorithms That Draw Botanical Trees
Tree algorithms explained: Ball Tree Algorithm vs. KD Tree vs. Brute Force
Understand what's behind the algorithms for structuring Data for Nearest Neighbour Search

All three are algorithms used for the Nearest Neighbour search. The Ball Tree and the KD Tree algorithm are tree algorithms used for spatial division of data points and their allocation into certain regions. In other words, they are used to structure data in a multidimensional space.
But first, let's start at the bottom: Why is it called a tree algorithm? What is a tree? — Skip, if you know it already!
A tree is a hierarchical way to structure data. As there exist linear data structures such as queues, where data is allocated one after another, trees are a common type of data structure. Trees are applied in many diverse fields of computer science, from graphics, over databases to operating systems. They do not only have the name in common with their botanical friends in nature, but also some characteristics. As botanical trees, the trees in computer science have roots, leaves, and branches. However, the allocation of these parts is bottom-up compared to normal trees. The roots are at the top of the tree and the leaves are at the lower end.
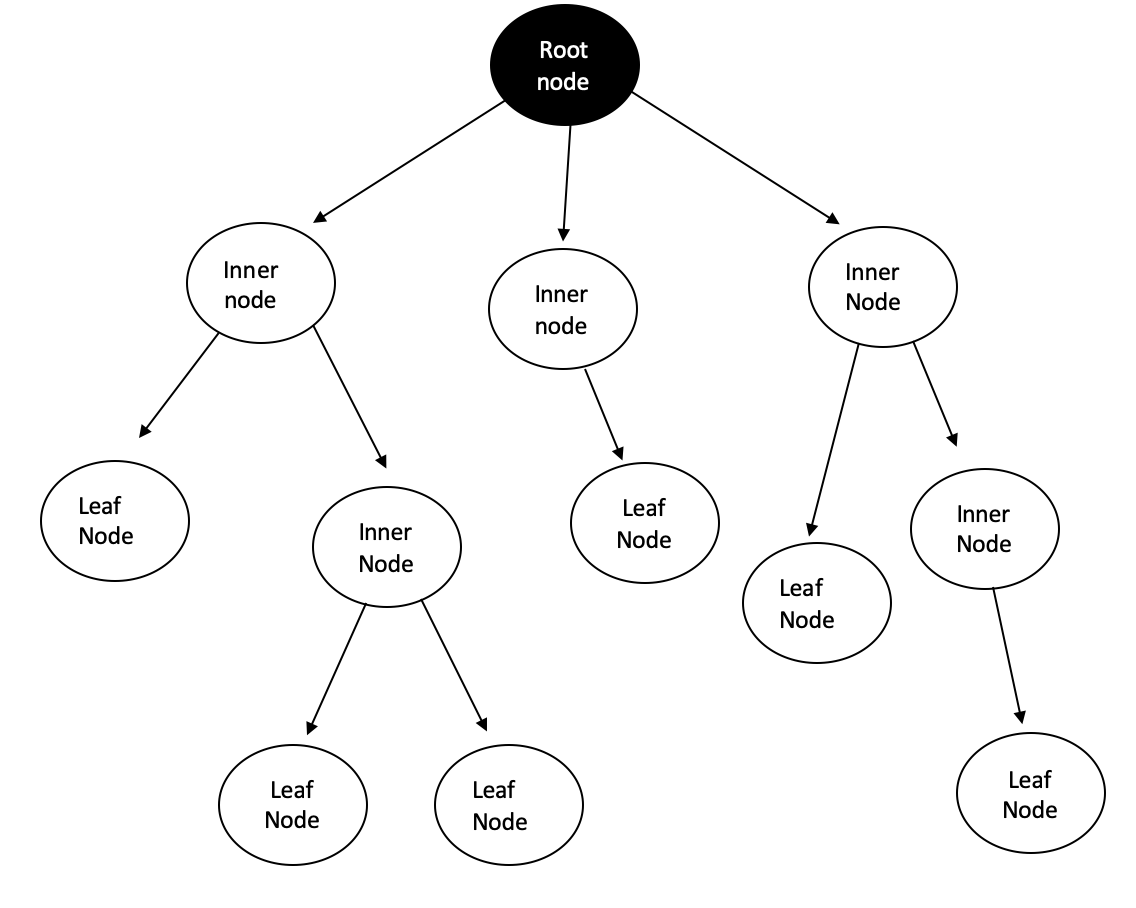
Parent Node = Is the node above another node, e.g. the root node is the parent node for the inner nodes below
Child node = As the name states, the children of a parent node and followingly, the nodes below a parent node. A child node can be again the parent node for the nodes below.
Root Node = The uppermost node, the origin of the tree
Leaf Node = Is also called an external node and can be seen as a "dead-end", it is the last node and has no child nodes below
Inner Node = Also called an internal node or branch node. It is a node that has a connection above and below (a child and parent node)
You are not yet on Medium? It costs only 4,16$ per month.
Get started
For a better understanding of how this can look like in a computer science topic, you can find below an HTML-code. A tree helps to structure a website and websites can normally be depicted using a tree.
<html>
<head>
<meta charset=utf-8" />
<title>Ball Tree vs. KD Tree</title>
<nav>
<a href="/r/">R</a>
<a href="/js/">JavaScript</a>
<a href="/python/">Python</a>
</nav>
</head> <body>
<h1>What is a tree?</h1>
<ul>
<li>List item one</li>
<li>List item two</li>
</ul>
<h2>How does a tree look like?</h2>
</body>
</html>

KD-Tree algorithm and the Ball algorithm are both binary algorithms to build such a tree. Binary means in this context, that each parent node only has two child nodes. Typically the algorithms are applied in Nearest Neighbour Search.
Ball Tree Algorithm
The Ball Tree Algorithm can be contemplated as a metric tree. Metric trees organize and structure data points considering the metric space in which the points are located. Using metrics the points do not need to be finite-dimensional or in vectors (Kumar, Zhang & Nayar, 2008).
The algorithm divides the data points into two clusters. Each cluster is encompassed by a circle(2D) or a sphere(3D). The sphere is often called a hypersphere.
"A hypersphere is the set of points at a constant distance from a given point called its center." — Wikipedia
From the sphere form of the cluster, the name Ball tree algorithm is derived. Each cluster represents a node of the tree. Let's see how the algorithm is executed.
The children are chosen to have maximum distance between them, typically using the following construction at each level of the tree.
First, the centroid of the whole cloud of data points is set. The point with the maximum distance to the centroid is selected as the center of the first cluster and child node. The point furthest away from the center of the first cluster is chosen as the center point of the second cluster. All other data points are then assigned to the node and cluster to the closest center, either being cluster 1 or cluster 2. Any point can only be a member of one cluster. The sphere lines can intersect each other, but the points must be clearly assigned to one cluster. If a point is exactly in the middle of both centers and has followingly the same distance to both sides, it has to be assigned to one cluster. The clusters can be unbalanced. That is basically the concept behind the Ball Tree Algorithm. The process of dividing the data points into two clusters/spheres is repeated within each cluster until a defined depth is reached. This leads to a nested cluster containing more and more circles.

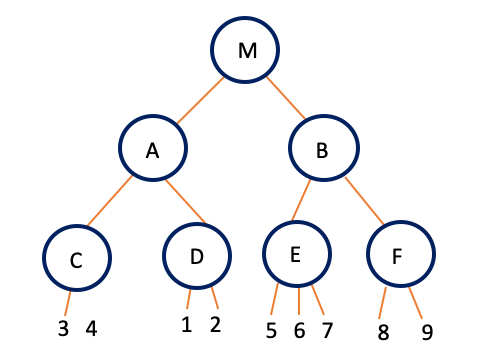
As can be seen in the graphic above the Tree has a depth of 2. Centroid 1 is the start of the algorithm. A Sphere (2D) is laid around all data points (grey color). From the center, the furthest distant point of a cluster is selected, which is here number 3 or number 9. This is the new center of Cluster 1, here number 3 for the purple cluster. The furthest distant point from point number three is the center of cluster 2. This is number 9 for the orange cluster. All data points comprised of the purple sphere are then considered for the calculation of the new Centroid 2. The same is done for all data points lying in the orange sphere, resulting in Centroid 3. The furthest distant points are then again the center of their new cluster. Datapoint number 3 is the furthest distant point from Centroid 2 and the center for the new cluster.
On the other side of Centroid 2, the greatest distance ist between it and data point number 1. It is the center of the second Cluster. This step is then also executed for the orange side, resulting again in two clusters. However, the orange side is unbalanced.
The resulting tree can be seen below (M is the sphere of Centroid 1 and the starting sphere encompassing all data points). From there the clusters are divided with depth 2:
KD Tree Algorithm
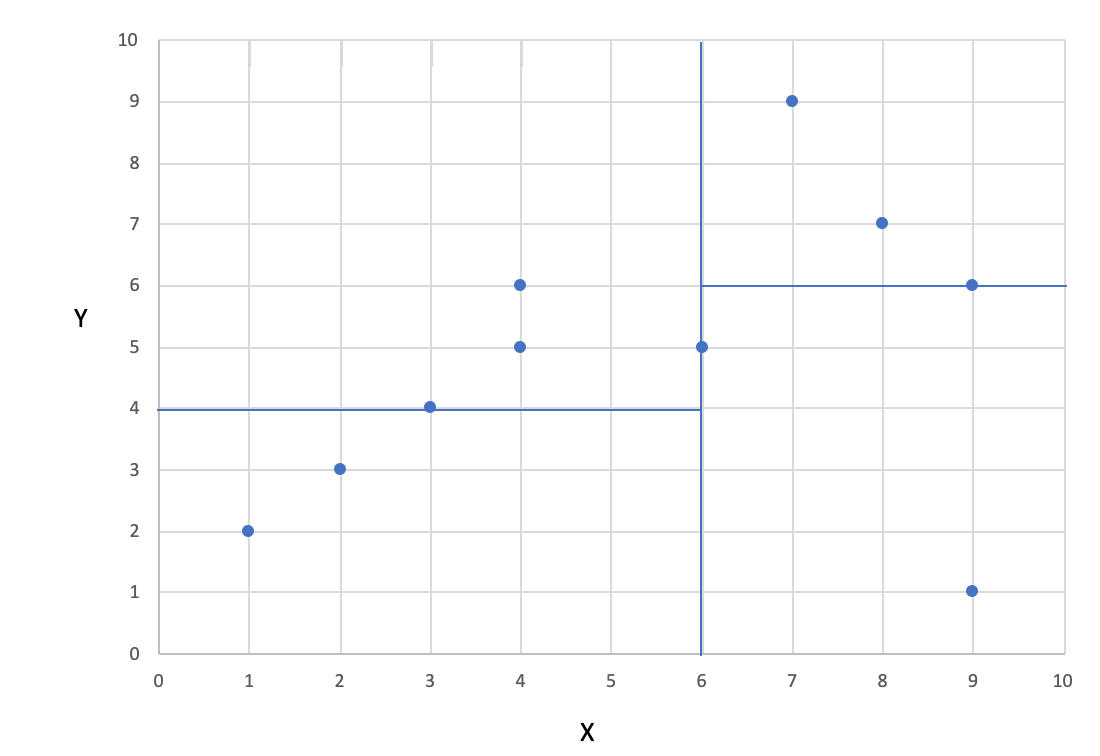
The KD Tree Algorithm is one of the most commonly used Nearest Neighbor Algorithms. The data points are split at each node into two sets. Like the previous algorithm, the KD Tree is also a binary tree algorithm always ending in a maximum of two nodes. The split criteria chosen are often the median. On the right side of the image below, you can see the exact position of the data points, on the left side the spatial position of them.
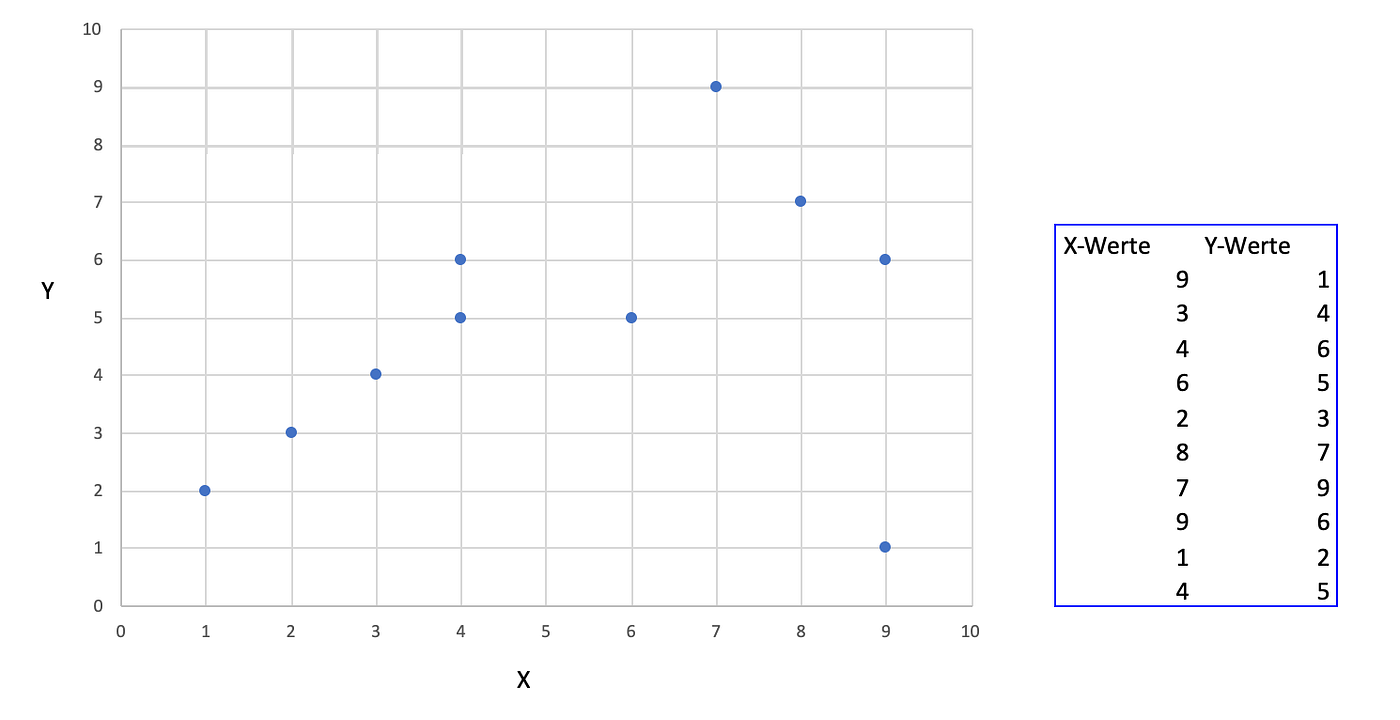
The KD-Tree Algorithm uses first the median of the first axis and then, in the second layer, the median of the second axis. We'll start with axis X.
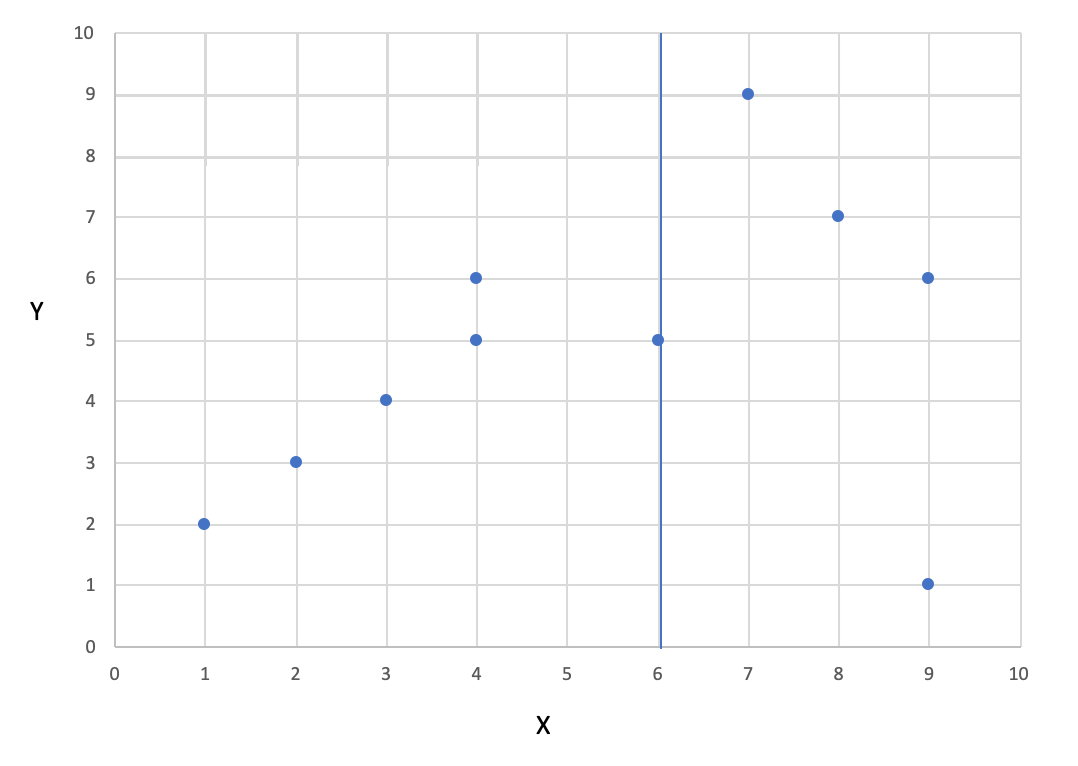
The in ascending order sorted x-values are: 1,2,3,4,4,6,7,8,9,9. Followingly, the median is 6.
The data points are then divided into smaller and bigger equal to 6. This leads to (1,2) (2,3) (3,4) (4,5) (4,6) on the left side and (6,5) (7,9) (8,7) (9,6) (9,1) on the cluster of the other side. Drawing the median of 6 in the coordinate system shows us, the two visualized clusters.
Now we're going to use the Y-Axis. We have already two clusters, so we need to take a look at them separately. On the left side, we got the sorted y-values: 2,3,4,5,6. The median is then 4. This leads to a separation line at value 4 and the coordinate system looks like:

The values are followingly separated at 4 and the first cluster contains (2,3) (1,2). The second cluster contains the points (4,6) (3,4) (4,5).
On the other side of the x-median of 4 are currently 5 points (including the point (5,6)). In sorted order, the y-values are 6,7,8,9,9. This leads to a median of 8 and the first cluster contains (9,1) and (6,5). The second cluster contains (8,7)(7,9)(9,6).
The resulting final coordinate system can be seen below. The data points have been divided into 4 clusters with a depth of 2 (X and Y).
But, how does the tree look like? Let's see how the resulting tree is divided.

Comparison and Summary
Brute Force may be the most accurate method due to the consideration of all data points. Hence, no data point is assigned to a false cluster. For small data sets, Brute Force is justifiable, however, for increasing data the KD or Ball Tree is better alternatives due to their speed and efficiency.
The KD-tree and its variants can be termed "projective trees," meaning that they categorize points based on their projection into some lower-dimensional space. (Kumar, Zhang & Nayar, 2008)
For low-dimensional data, the KD Tree Algorithm might be the best solution. As seen above, the node divisions of the KD Tree are axis-aligned and cannot take a different shape. So the distribution might not be correctly mapped, leading to poor performance.
For a high-dimensional space, the Ball Tree Algorithm might be the best solution. Its performance depends on the amount of training data, the dimensionality, and the structure of the data. Having many data points that are noise can also lead to a bad performance due to no clear structure.
Thanks for reading, I hope you enjoyed it!
higginbothammothip.blogspot.com
Source: https://towardsdatascience.com/tree-algorithms-explained-ball-tree-algorithm-vs-kd-tree-vs-brute-force-9746debcd940
0 Response to "Computer Algorithms That Draw Botanical Trees"
Post a Comment